Ön nyilván arra kíváncsi, ki fog nyerni. Ezt azonban nélkülem is tudja. Az elektor.hu előrejelzései, bár a tudományos szaknyelvben „jóslatnak” nevezik, nem varázsgömbben születnek. Az alábbi videón Richard Feynman Nobel díjas fizikus egy percben megmutatja, hogyan.
2017-ben négy nappal a németországi választások előtt 4 előrejelzést tettem közzé az eredményekre. Mind a négy 100 %-ban bejött. Azért, mert előtte gondosan elemeztem a német választási rendszert. Először adatokat gyűjtöttem, vagyis megnéztem az eggyel korábbi választás eredményét.
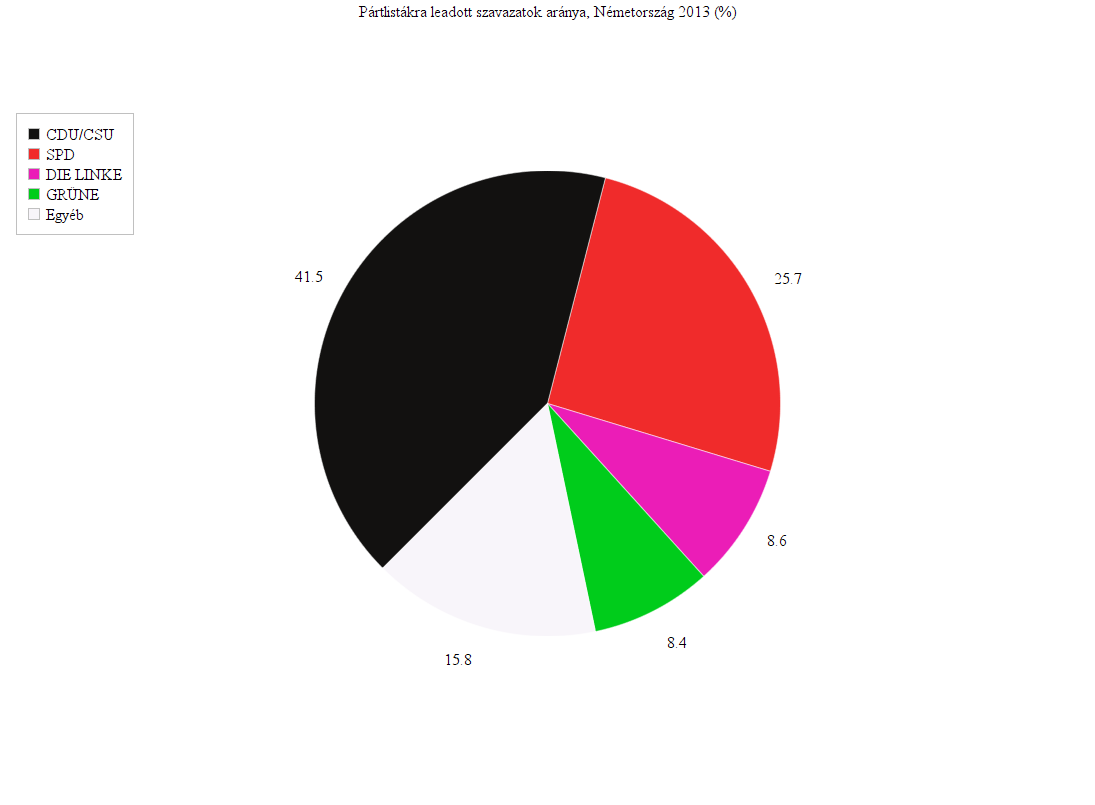
Az ábra egy, a matematikai tanulmányainkból ismert halmaz, amelynek a szavazatok az elemei. Az egyes voksoknak lehetnek közös tulajdonságai, például az, hogy ugyanarra a pártra adták le őket. Így a halmazon belül a szavazatokat részhalmazokba csoportosíthatjuk. A választás hivatalos eredményéből valamennyinek pontosan ismerjük az elemszámát. A rendszerben azonban van egy másik halmaz is, a parlamenti mandátumoké.
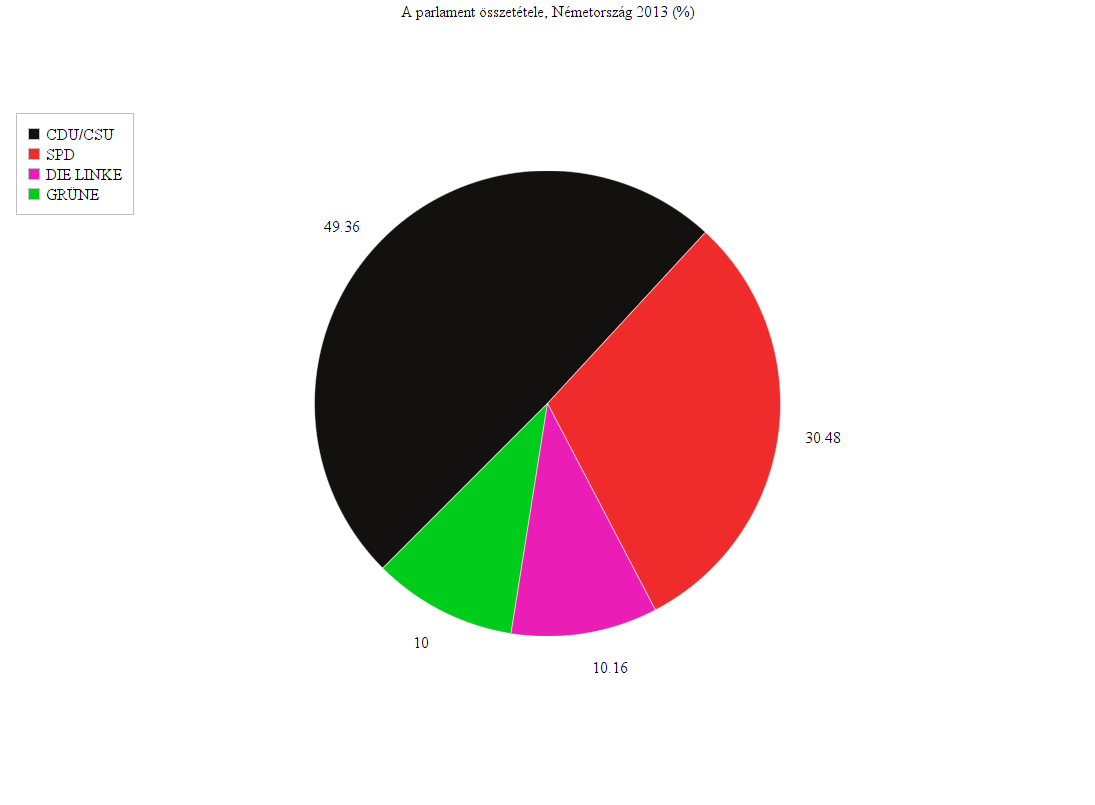
Ennek elemei a képviselői helyek, melyeket ugyancsak részhalmazokba csoportosíthatunk közös tulajdonságaik alapján, vagyis aszerint, hogy melyik párt kapta meg az adott mandátumot. Itt is pontosan ismerjük az egyes részhalmazok és a halmaz elemszámát.
Ahogy Feynman mondta, a természet törvényeit először találgatással próbáljuk megállapítani. Választási rendszerek esetében az első tippünk, hogy a mandátumok halmaza a szavazatokéból származik. Ez nyilvánvalónak tűnik, de muszáj bizonyítani, amitől itt hely hiányában eltekintek. (Ha nem hisznek nekem, olvassák el ezt.)
Az első problémánk, hogy míg a szavazatok halmazának több millió, addig a mandátumokénak csak néhány száz eleme van. Tehát nem lehet őket egy az egyben összepárosítani, és kideríteni, hogyan lesz egyikből a másik. Ezen azonban egyszerűen segíthetünk: az egyes részhalmazok elemszámát elosztjuk a teljes halmaz elemszámával, így a végén százalékokat kapunk mindkét halmazban. Most már tudunk számolni, és kinyomozhatjuk, hogyan keletkezett a mandátumok halmaza a szavazatokéból. Keressük meg a két ábra közti különbségeket!


A legszembetűnőbb, hogy a felsőben szerepel egy fehér színű részhalmaz, ami hiányzik az alsóból. A másik különbség, hogy az összes többi részhalmaz mérete nagyobb az alsó, mint a felső halmazban.
Mivel más különbség nincs, találgassunk újra! Lehetséges, hogy a két dolog összefügg egymással? Vagyis, hogy a fehér részhalmaz eltűnése és a többi méretének növekedése kapcsolatban áll? Hogy megtudjuk, muszáj lesz számolnunk!
A fehér részhalmazhoz rendelt érték a felső ábrán 15,8 (százalék, amely a részhalmaz elemszámáról ad információt). Az a tény, hogy a fehér részhalmaz nem látható az alsó ábrán úgy is leírható, hogy ott van ugyan, de az elemszáma nulla. Van tehát két értékünk, amelyből kiszámolhatjuk, mi történt a fehér részhalmazzal:
0 – 15,8 = -15,8
Most már ismerjük a fehér részhalmaz elemeinek történetét: kivonták őket a rendszerből. A művelet, amit kerestünk:
-15,8
Nézzük, mi történt a többi részhalmazzal. Ezek együttes értéke a felső ábrán 84,2, az alsón 100.
100 – 84,2 = 15,8
Már azt is tudjuk, mi történt az összes többi részhalmaz elemeivel. A művelet:
+15,8
Van tehát egyszer -15,8 és egyszer +15,8. Úgy tűnik, igazunk volt, amikor azt feltételeztük, hogy a fehér részhalmaz „eltűnése” és az összes többi méretének növekedése összefügg egymással. A folyamatot leírhatjuk így:
A fehér elemei tehát nem tűntek el, egyszerűen újra elosztották őket a többi részhalmaz között. Ha elvégezzük a számításokat, akkor kiderül, hogy az elemeket arányosan osztották újra: minél nagyobb volt egy részhalmaz a szavazatok halmazában, annál több elemet kapott a fehér részhalmaz elemeiből. Ha így van, akkor lehet egy újabb tippünk:
Vagyis amennyiszer nagyobb a fekete, mint a piros a szavazatok halmazában, ugyanannyiszor nagyobb a mandátumokéban. Tippünket ismét számolással ellenőrizhetjük.
Szavazatok halmaza: fekete / piros = 41,5 / 25,7 = 1,61
Mandátumok halmaza: fekete / piros = 49,36 / 30,48 = 1,61
1,61 = 1,61
Ugyanennek igaznak kell lennie bármely két részhalmazra, amely szerepel mind a szavazatok, mind a mandátumok halmazában. Próbaképpen nézzük meg a pirosat és a zöldet.
Szavazatok halmaza: piros / zöld = 25,7 / 8,4 = 3,05
Mandátumok halmaza: piros / zöld = 30,48 / 10 = 3,04
3,05 ~ 3,04
A hányadosok között nagyon pici különbséget látunk, de ennek pontosan ismerjük az okát. Talán még emlékeznek, hogy a szavazatok halmazának több millió, míg a mandátumokénak csak néhány száz eleme van. Amikor átváltjuk egyiket a másikra, akkor jó eséllyel tört szám lesz az eredmény. Például azt kapjuk, hogy egy pártnak 25,6 mandátum jár. Mivel azonban a képviselők emberek, az eredményt kerekíteni kell felfelé, vagy lefelé. Ez okozza az apró eltéréseket a hányadosok között.
Elvégezve a számításokat megállapíthatunk egy a szabályt a 2013-as német választás eredményére:
Ha háromszor annyian szavaztak rá, akkor háromszor annyi képviselői helyet kap. Ha 1,61-szer, akkor 1,61-szer. És így tovább. Hogy tovább egyszerűsítsünk, felírhatjuk egyenletben is:
Psz / P’sz = Pm / P’m
Ahol P és P’ olyan pártokat jelent, amelyek bekerültek a parlamentbe, „sz” a szavazatok számát (vagy arányát), míg „m” a mandátumok számát (vagy arányát) jelöli. Az egyenlet megoldható a 2013-as németországi választás eredményén bármely két parlamentbe bekerült pártra. De vajon igaz bármely országos parlamenti választás eredményére Németországban?
Ez kulcskérdés, mert ha a válasz igen, akkor megtaláltuk a német választási rendszer egy szabályát éppen úgy, ahogy a fizikusok rábukkannak a természet valamely törvényére. A döntéshez meg kell vizsgálnunk részletesen, hogyan osztják a mandátumokat Németországban. Mivel ez a munka több hónapig is eltarthat, ebben a cikkben kénytelenek vagyunk eltekinteni tőle, de aki kíváncsi elolvashat egy rövid összefoglalót itt, egy részletesebbet itt (9-18. oldal), vagy a teljes német választási törvényt itt.
Ebből kiderül, hogy a német mandátum kiosztási módszer miatt bármely választási eredményre igaz kell legyen az egyenletünk: Psz / P’sz = Pm / P’m.
Van egy szabályunk, de még nem dőlhetünk hátra. Richard Feynmantól tudjuk, hogy bármilyen szép egy elmélet, ha nem egyezik a kísérleti adatokkal, akkor rossz.
Ezért tettem közzé 2017. szeptember 20-án a következő előrejelzést a német választás eredményére:
Négy nappal később megtartották a választást Németországban, és az eredményt összehasonlítottam az előrejelzéssel. Tökéletesen stimmelt. Bármely két parlamentbe bekerült pártot helyettesítem be az egyenletbe mindig (majdnem) egyenlőséget kapok. Ezt ön is ellenőrizhető itt. Hasonló módszerrel a németországi választásra további három előrejelzést tettem közzé, ezek szintén 100 %-ban egyeznek az adatokkal.
Tessék jól megjegyezni ezt a mondatot, mert kulcsfontosságú a magyar választási rendszerrel kapcsolatban is. Tudjuk, hogy Németországban nem véletlenszerűen egyenlő a parlamentbe bekerült pártok szavazatainak és mandátumainak a hányadosa. A választási rendszerükből következően muszáj, hogy egyenlő legyen. Mivel ezt előre tudtuk jelezni, és az előrejelzést össze tudtuk hasonlítani a megfigyelési adatokkal, bizonyítékunk van rá, hogy az elméletünk helyes. A 2017-es német választás eredménye cáfolhatta volna az elméletünket, de nem ez történt: az adatok igazolják az elméletet. Ez, és csakis ez dönt arról, hogy a szabály, amit találtunk helyes, vagy nem.
Azért hangsúlyozom ezt ennyire didaktikusan, mert a magyar választási rendszerre szóló elméletünkről sokan elmondják majd a véleményüket pro és kontra. Ennek azonban a világon semmi jelentősége nincs. Mindegy mit gondolnak a szakértők, mit gondol ön, vagy én. Ha az adatok egyeznek az előrejelzésekkel, akkor bizonyítékunk van arra, hogy az elmélet helyes. Ha nem egyeznek, akkor meg arra, hogy az elmélet rossz.
Ha eljutottak eddig az olvasásban, akkor már tudják, hogyan tudtam előre jelezni 2017-ben hat választás eredményét, és azt is, hogyan teszem meg ugyanezt a 2018-as magyarországi választással. Az első lépés az adatgyűjtés. Nézzük az eggyel korábbi, a 2014-es választás eredményét.
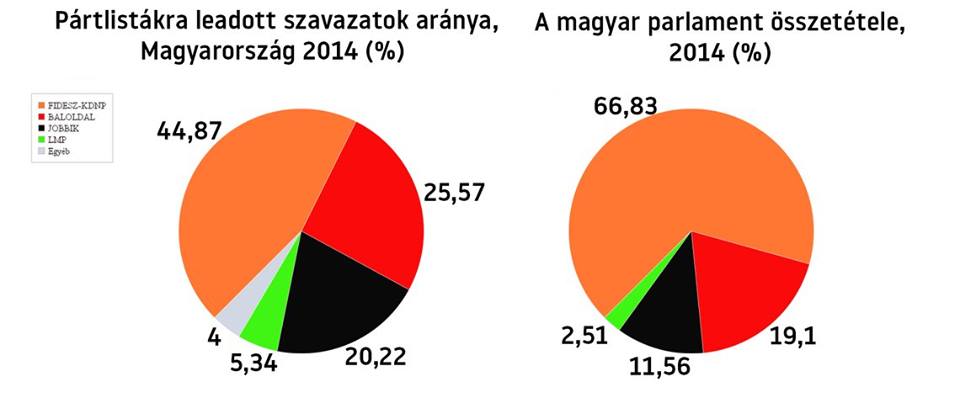
A különbségeket keresve elsőre itt is feltűnik, hogy a fehér részhalmaz „eltűnt” a rendszerből. Azonban az már nem igaz, hogy az összes többi mérete nagyobb lett. Csak a narancssárga lett nagyobb, a piros, a fekete és a zöld mérete csökkent.
Ez látszólag három különbség, valójában csak kettő. A fehér részhalmazt most is kezelhetjük úgy, mint ami ott van a mandátumok halmazában, de az elemszáma nulla. Így erre is igaz, hogy a mérete kisebb lett. Tehát két különbséget azonosíthatunk:
Tippünket, hogy a két dolog összefügg egymással számolással ellenőrizhetjük. A narancssárga értéke a mandátumok halmazában 66,83, a szavazatokéban 44,87.
66,83 – 44,87 = 21,96
A narancssárga részhalmazon elvégzett művelet:
+21,96
Az összes többi részhalmaz együttes értéke a mandátumok halmazában 33,17, a szavazatokéban 55,13.
33,17 – 55,13 = -21,96
A piros, a fekete, a zöld és a fehér részhalmazon elvégzett művelet:
-21,96
Van egyszer +21,96 és egyszer -21,96. Úgy tűnik, igazunk volt, amikor feltételeztük, hogy a két folyamat, a narancssárga részhalmaz méretének növekedése, valamint az összes többi méretének csökkenése, összefügg egymással. A műveletet leírhatjuk így:
Így a négy részhalmaz összesen 21,96 (százaléknyi) eleme nem tűnt el a rendszerből, helyette újraosztották oly módon, hogy minden egyes kivont elemet hozzáadták a narancssárga részhalmazhoz.
Próbáljuk megoldani a német rendszernél felfedezett egyenletet a 2014-es magyarországi választás eredményére. Eszerint bármely két parlamentbe bekerült párt szavazatainak és mandátumainak a hányadosa egyenlő kellene, hogy legyen:
44,87 / 25,57 = 1,75 66,83 / 19,1 = 3,49
1,75 ≠ 3,49
44,87 / 20,22 = 2,22 66,83 / 11,56 = 5,78
2,22 ≠ 5,78
44,87 / 5,34 = 8,4 66,83 / 2,51 = 26,63
8,4 ≠ 26,63
Nem működik, és ez megerősíti azt, amit már a halmazok összehasonlításánál is láttunk. Ez egyértelmű bizonyíték arra, hogy a német és a magyar választási rendszer különbözik egymástól, ami azt illeti, nagyon különbözik. De vajon fel tudunk –e írni egy másik egyenletet, vagyis találunk –e bármilyen szabályosságot a magyar eredményekben?
Ha rápillantunk a fenti számokra, akkor azt látjuk, hogy a jobboldali hányadosok mindig nagyobbak, mint a baloldaliak. Mivel az osztások számlálójában mindig ugyanaz a párt szerepel, a Fidesz, a nevezőjébe pedig bármely másik pártot behelyettesíthetjük, felírhatunk egy szabályt a 2014-es magyarországi választás eredményére:
Fsz / Psz < Fm / Pm
Ahol „F” a FIDESZ – KDNP, „P” bármely másik párt, „sz” a szavazatok száma (vagy aránya), „m” a parlamenti mandátumok száma (vagy aránya). De vajon igaz –e az egyenlőtlenség bármely magyarországi választás eredményére?
Más megfogalmazással az a kérdés, hogy az egyenlőtlenség elemei felcserélhetőek –e. Helyet cserélhet –e a számlálóban szereplő „F” és a nevezőben lévő „P”? Illetve megfordulhat –e a relációs jel?
Így a könnyen odavetett válaszok helyett illik komolyan venni.
A választási rendszerek, így a magyar is, alapvetően két pilléren állnak.
Ha Magyarországon figyelmen kívül hagynánk az utóbbit (amit természetesen nem tehetünk meg), akkor a fenti kérdésre a válasz igen lenne. A kampányszabályozással együtt azonban ezzel éppen ellentétes következtetésre jutunk: az egyenlőtlenség elemei nem felcserélhetőek.
Ez egy elmélet, amely tökéletesen egyezik a rendelkezésünkre álló adatokkal, vagyis a jelenleg érvényes választási rendszerben megtartott eddigi egyetlen országgyűlési választás eredményével. Sokkal erősebb bizonyítékot szolgáltat azonban az, ha képesek vagyunk előre megmondani a 2018-as választások eredményét.
Az elektor.hu a következő hetekben nyolc előrejelzést tesz közzé. Valamennyi a 2018-as magyarországi országgyűlési választás eredményéből, illetve az azt megelőző kampányból következő adatokra vonatkozik. Öt a mandátumok kiosztására, három a kampányra. Mind a nyolc a hivatkozott elméletből következik. Eszerint a választás eredményéből és a kampányból következő adatoknak egyezniük kell mind a nyolc előrejelzéssel. Ha így lesz, akkor az bizonyítja, hogy az Fsz / Pm < Fm / Pm egyenlőtlenség igaz bármely magyarországi országgyűlési választás eredményére a jelenlegi választási rendszerben.
A módszer már több próbát kiállt, 2017-ben hat választás eredményét jeleztem előre, és teszteltem:
Hollandia itt.
Egyesült Királyság itt.
Franciaország itt.
Németország és Új-Zéland itt.
Ausztria itt.
Név: Bánovics Attila
Email: info@elektor.hu